Théorème de Hadamard-Lévy : Différence entre versions
De AgregmathKL
(Page créée avec « Ce développement montre l'équivalence pour une fonction de classe <math>\mathcal{C}^2</math> entre être un <math>\mathcal{C}^1</math>-difféomorphisme et être un difféom... ») |
|||
| (2 révisions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 5 : | Ligne 5 : | ||
== Recasements == | == Recasements == | ||
| − | * | + | * [[203 -- Utilisation de la notion de compacité.]] |
| + | * [[204 -- Connexité. Exemples et applications.]] | ||
| + | * [[214 -- Théorème d'inversion locale, théorème des fonctions implicites. Exemples et applications.]] | ||
| + | * [[215 -- Applications différentiables définies sur un ouvert de Rn. Exemples et applications.]] | ||
| + | * [[220 -- Équations différentielles X' = f(t,X). Exemples d'étude des solutions en dimension 1 et 2.]] | ||
| + | * (?) | ||
== Références == | == Références == | ||
* Zuily-Queffelec p.400 | * Zuily-Queffelec p.400 | ||
| + | |||
| + | |||
| + | [[Category: Développement de la leçon 203]] | ||
| + | [[Category: Développement de la leçon 204]] | ||
| + | [[Category: Développement de la leçon 214]] | ||
| + | [[Category: Développement de la leçon 215]] | ||
| + | [[Category: Développement de la leçon 220]] | ||
Version actuelle en date du 16 décembre 2014 à 15:37
Ce développement montre l'équivalence pour une fonction de classe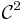 
entre être un 
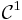-difféomorphisme et être un difféomorphisme local propre.
Le développement
pdf : Fichier:Hadamard-Levy.pdf
Recasements
- 203 -- Utilisation de la notion de compacité.
- 204 -- Connexité. Exemples et applications.
- 214 -- Théorème d'inversion locale, théorème des fonctions implicites. Exemples et applications.
- 215 -- Applications différentiables définies sur un ouvert de Rn. Exemples et applications.
- 220 -- Équations différentielles X' = f(t,X). Exemples d'étude des solutions en dimension 1 et 2.
- (?)
Références
- Zuily-Queffelec p.400
