Théorème de Hahn-Banach : Différence entre versions
De AgregmathKL
m (a déplacé Théorème de Hahn-Banach en dimension finie vers Théorème de Hahn-Banach) |
(→Hahn-Banach analytique en dimension infinie) |
||
| (Une révision intermédiaire par le même utilisateur non affichée) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | == | + | == Hahn-Banach géométrique en dimension finie == |
[[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:HahnBanachGéom.pdf | Hahn-Banach géométrique en dimension finie]] | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:HahnBanachGéom.pdf | Hahn-Banach géométrique en dimension finie]] | ||
| Ligne 21 : | Ligne 21 : | ||
# Apparemment il y a d'autres références, un Oraux X-ENS et Objectif Agrégation (à vérifier). | # Apparemment il y a d'autres références, un Oraux X-ENS et Objectif Agrégation (à vérifier). | ||
| − | == Hahn-Banach | + | == Hahn-Banach en dimension infinie == |
| − | + | On montre ici le théorème de Hahn-Banach analytique en dimension infinie et on en déduit Hahn-Banach géométrique. On montre aussi plusieurs corollaires de Hahn-Banach analytique. | |
| − | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:HahnBanach_diminfini.tex | Hahn-Banach | + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:HahnBanach_diminfini.pdf | Hahn-Banach en dimension infinie]] |
| + | |||
| + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:HahnBanach_diminfini.tex | Hahn-Banach en dimension infinie]] | ||
Référence : Analyse fonctionnelle, de Brezis. | Référence : Analyse fonctionnelle, de Brezis. | ||
Version actuelle en date du 4 octobre 2013 à 13:52
Hahn-Banach géométrique en dimension finie
Hahn-Banach géométrique en dimension finie
Hahn-Banach géométrique en dimension finie
Référence :
- Géométrie, de Tauvel, à savoir qu'il y a des coquilles dans la démonstration :
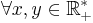et non 
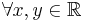pour la démonstration de la convexité. De plus Tauvel ne montre pas le lemme technique donné dans le pdf. - Il y a d'autres références ; citons par exemple Ramis-Warusfel.
Hahn-Banach analytique en dimension finie
Hahn-Banach analytique en dimension finie
Hahn-Banach analytique en dimension finie
Référence :
- Petit guide de calcul différentiel, de Rouvière.
- Apparemment il y a d'autres références, un Oraux X-ENS et Objectif Agrégation (à vérifier).
Hahn-Banach en dimension infinie
On montre ici le théorème de Hahn-Banach analytique en dimension infinie et on en déduit Hahn-Banach géométrique. On montre aussi plusieurs corollaires de Hahn-Banach analytique.
Hahn-Banach en dimension infinie
Hahn-Banach en dimension infinie
Référence : Analyse fonctionnelle, de Brezis.
