Décomposition de Dunford : Différence entre versions
De AgregmathKL
(ajout d'une version avec des notations intéressante et qui n'a pas de référence : je me suis dit qu'il était dommage qu'elle soit introuvable si on n'a pas eu Matthieu en prof.) |
|||
| Ligne 1 : | Ligne 1 : | ||
| − | La décomposition de Dunford d'une matrice est une unique façon de l'écrire comme somme d'une matrice diagonalisable et d'une matrice nilpotente qui commutent. | + | La décomposition de Dunford d'une matrice est une unique façon de l'écrire comme somme d'une matrice diagonalisable et d'une matrice nilpotente qui commutent. Il y a plusieurs versions de la preuve. |
== Preuve de l'existence et unicité == | == Preuve de l'existence et unicité == | ||
| − | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Dunford.pdf | Décomposition de Dunford ( Girand 2012 )]] | + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Dunford.pdf | Décomposition de Dunford (Girand 2012)]] |
[[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:dunford.tex | Décomposition de Dunford et application à <math>A</math> diagonalisable <math>\Leftrightarrow \; \exp(A)</math> diagonalisable (2011) ]] | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:dunford.tex | Décomposition de Dunford et application à <math>A</math> diagonalisable <math>\Leftrightarrow \; \exp(A)</math> diagonalisable (2011) ]] | ||
| − | == Construction effective via la méthode de Newton | + | == Construction effective via la méthode de Newton == |
| − | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Dunford_effective.pdf | Décomposition de Dunford effective ( Pillet 2012 )]] | + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Dunford_effective.pdf | Décomposition de Dunford effective (Pillet 2012)]] (avec remarques sur la complexité) |
| − | + | ||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:NewJorCheDun.pdf | Décomposition de Dunford effective (2021)]] (version manuscrite avec les notations en grand O de Matthieu Romagny) | ||
[[Category:Développement de la leçon 153]] | [[Category:Développement de la leçon 153]] | ||
[[Category:Développement de la leçon 157]] | [[Category:Développement de la leçon 157]] | ||
Version actuelle en date du 18 mars 2021 à 20:02
La décomposition de Dunford d'une matrice est une unique façon de l'écrire comme somme d'une matrice diagonalisable et d'une matrice nilpotente qui commutent. Il y a plusieurs versions de la preuve.
Preuve de l'existence et unicité
Décomposition de Dunford (Girand 2012)
Décomposition de Dunford et application à 
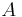diagonalisable 
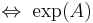diagonalisable (2011)
Construction effective via la méthode de Newton
Décomposition de Dunford effective (Pillet 2012) (avec remarques sur la complexité)
Décomposition de Dunford effective (2021) (version manuscrite avec les notations en grand O de Matthieu Romagny)
