Théorème de Fejér : Différence entre versions
De AgregmathKL
(Page créée avec « Ce développement exhibe une suite de polynômes trigonométriques convergeant uniformément vers une fonction continue <math>2\pi</math>-périodique, et un moyen de la const... ») |
|||
| Ligne 11 : | Ligne 11 : | ||
* Hirsh-Lacombe, '''Éléments d'analyse fonctionnelle''' 1997 ( p.32, exercice 2c) | * Hirsh-Lacombe, '''Éléments d'analyse fonctionnelle''' 1997 ( p.32, exercice 2c) | ||
* Zuily-Queffélec, '''Éléments d'analyse pour l'agrégation''' | * Zuily-Queffélec, '''Éléments d'analyse pour l'agrégation''' | ||
| + | |||
| + | |||
| + | [[Category:Développement de la leçon 240]] | ||
| + | [[Category:Développement de la leçon 246]] | ||
Version actuelle en date du 16 décembre 2014 à 15:33
Ce développement exhibe une suite de polynômes trigonométriques convergeant uniformément vers une fonction continue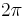 
-périodique, et un moyen de la construire (par convolution avec le noyau de Fejér).
Le développement
pdf : Fichier:Fejér.pdf
Recasements
- 240 -- Transformation de Fourier, produit de convolution. Applications.
- 246 -- Séries de Fourier. Exemples et applications.
Références
- Hirsh-Lacombe, Éléments d'analyse fonctionnelle 1997 ( p.32, exercice 2c)
- Zuily-Queffélec, Éléments d'analyse pour l'agrégation
