Développements par thèmes : Différence entre versions
De AgregmathKL
(→Équations différentielles) |
(→Intégration) |
||
| Ligne 122 : | Ligne 122 : | ||
=== Intégration === | === Intégration === | ||
* Critère de Weyl ([[Fichier:Tex.png|alt=Tex|link=Média: Critere_Weyl.tex |24px]], [[Fichier:Pdf.png|alt=Pdf|link=Média: Critere_Weyl.pdf |24px]]) | * Critère de Weyl ([[Fichier:Tex.png|alt=Tex|link=Média: Critere_Weyl.tex |24px]], [[Fichier:Pdf.png|alt=Pdf|link=Média: Critere_Weyl.pdf |24px]]) | ||
| − | * [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Calcul_integrale. | + | * Un exemple de calcul d'intégrale ([[Fichier:Tex.png|alt=Tex|link=Média:Calcul_integrale.tex |24px]], [[Fichier:Pdf.png|alt=Pdf|link=Média:Calcul_integrale.pdf |24px]]) |
* [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:E-Mcb.pdf | Formule sommatoire d'Euler Maclaurin]] | * [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:E-Mcb.pdf | Formule sommatoire d'Euler Maclaurin]] | ||
* [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Poisson.pdf | Formule Sommatoire de Poisson]] | * [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Poisson.pdf | Formule Sommatoire de Poisson]] | ||
| − | * [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Formule_complements. | + | * Formule des compléments ([[Fichier:Tex.png|alt=Tex|link=Média:Formule_complements.tex |24px]], [[Fichier:Pdf.png|alt=Pdf|link=Média:Formule_complements.pdf |24px]]) |
* [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Fourier.pdf | Formule d'inversion de Fourier]] | * [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Fourier.pdf | Formule d'inversion de Fourier]] | ||
* [[Intégrale de Fresnel]] | * [[Intégrale de Fresnel]] | ||
| − | * [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Methode_gauss. | + | * Méthode de Gauss d'approximation d'intégrale ([[Fichier:Tex.png|alt=Tex|link=Média:Methode_gauss.tex |24px]], [[Fichier:Pdf.png|alt=Tex|link=Média:Methode_gauss.pdf |24px]]) |
| − | * [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:MethodedeLaplace. | + | * Méthode de Laplace ([[Fichier:Tex.png|alt=Tex|link=Média:MethodedeLaplace.tex |24px]], [[Fichier:Pdf.png|alt=Pdf|link=Média:MethodedeLaplace.pdf |24px]]) |
| − | * [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:ProlongementGamma. | + | * Prolongement de la fonction <math>\Gamma</math> ([[Fichier:Tex.png|alt=Tex|link=Média:ProlongementGamma.tex |24px]], [[Fichier:Pdf.png|alt=Pdf|link=Média:ProlongementGamma.pdf |24px]]) |
| − | * [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Abel_angulaire. | + | * Théorème d'Abel angulaire ([[Fichier:Tex.png|alt=Tex|link=Média:Abel_angulaire.tex |24px]], [[Fichier:Pdf.png|alt=Pdf|link=Média:Abel_angulaire.pdf |24px]]) |
* [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Abel.pdf | Théorèmes d'Abel angulaire et taubérien faible]] | * [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Abel.pdf | Théorèmes d'Abel angulaire et taubérien faible]] | ||
* [[Théorème de Fejér]] | * [[Théorème de Fejér]] | ||
Version du 31 décembre 2012 à 14:24
Cette page liste tous les développements présents sur le site, triés par thèmes. Les doublons sont autorisés et même conseillés dans la mesure où la plupart des théorèmes sont à cheval entre plusieurs domaines.
Il est donc explicitement demandé à ceux qui ajoutent un développement de le faire apparaitre dans toutes les parties qui le concernent.
(le choix des découpages est arbitraire, toute modification éclairée est la bienvenue).
Si vous préférez vous pouvez toujours vous dépêtrer avec le fouillis de la permière version de cette page : Développements.
Sommaire
Algèbre
Algèbre linéaire, bilinéaire, réduction d'endomorphismes
- Commutant d'un endomorphisme (
, 
) - Convergence d'une suite de polygônes vers l'isobarycentre (, )
- Composantes connexes de l'ensemble des formes quadratiques non dégénérées.
- Décomposition de Bruhat
- Décomposition de Dunford
- Ellipsoïde de John-Lœwner
- Isomorphisme entre M_n(K) et son dual
- Lemme de Morse
- Orthodiagonalisation des endomorphismes auto-adjoints ( ; )
- Points extrémaux de la boule unité de L(E)
- Réduction des matrices normales (, )
- Sous-groupes compacts de
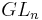
- Surjectivité de l'exponentielle (, )
- Théorème de Cartan-Dieudonné (, )
- Action du groupe modulaire sur le demi-plan de Poincaré
- Endomorphismes cycliques, invariants de similitude et réduction de Frobenius
Anneaux, arithmétique, dénombrement
- Automorphismes de
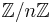(, ) - Décomposition de Dunford
- Nombres de Bell
- Groupes d'ordre pq ( ; )
- Sous groupes finis de
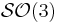(, ) - Une version faible du théorème de Dirichlet (, )
- Probabilité que deux entiers soient premiers entre eux
- Primalité des nombres de Mersenne
- Théorème de Gauß pour les polygones réguliers constructibles
- Théorème des deux carrés ( ; )
Géométrie
- Ellipse de Steiner ( ; )
- Convergence d'une suite de polygônes vers l'isobarycentre (, )
- Groupe circulaire ( ; )
- Le paradoxe de Banach-Tarski
- Points extrémaux de la boule unité de L(E)
- Simplicité de (, )
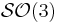- Sous groupes finis de (, )
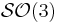- Théorème de Caratheodory ( ; )
- Théorème de Cartan-Dieudonné (, )
- Théorème de Hahn-Banach en dimension finie
- Théorème de Jordan (, )
- Théorème de Gauß pour les polygones réguliers constructibles
- Action du groupe modulaire sur le demi-plan de Poincaré
Théorie des corps, irréductibilité, primalité
- Irréductibilité des polynômes cyclotomiques ()
- Polynômes irréductibles sur
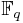(, ) - Théorème de d'Alembert-Gauss ( ; )
- Théorème de Kronecker ( ; )
- Théorème de l'élément primitif (, )
- Théorème de Wedderburn ()
- Primalité des nombres de Mersenne
- Théorème de Gauß pour les polygones réguliers constructibles
Théorie des groupes
- Automorphismes de (, )
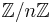- Décomposition de Bruhat
- Groupes d'ordre 12 (, )
- Théorème de Lie-Kolchin (, )
- Le paradoxe de Banach-Tarski
- Simplicité de
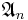( ; ) - Simplicité de (, )
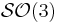- Sous-groupes compacts de
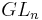
- Sous groupes finis de (, )
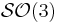- Théorème de Cartan-Von Neumann (, )
- Théorème de Burnside
- Théorème de Sylow ( ; )
- Théorème de Gauß pour les polygones réguliers constructibles
- Action du groupe modulaire sur le demi-plan de Poincaré
- Table de caractères de
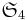( ; ) - Table de caractères de
( ; )
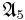Analyse
Analyse fonctionelle et distributions
- Densité des polynômes orthogonaux (, )
- Dérivée des fonctions lipschitziennes (, )
- Formule d'inversion de Fourier
- Projection dans un espace de Hilbert (, )
- Solution élémentaire de l'équation de Schrodinger
- Théorème de Cartan-Von Neumann (, )
- Théorème de Fejér
- Théorème de Hadamard-Lévy
- Théorème de Fischer - Riesz
- Un espace de Sobolev
Analyse numérique, méthodes d'approximation
- Dérivée des fonctions lipschitziennes (, )
- Méthode de Gauss d'approximation d'intégrale (, )
- Méthode de Newton
Calcul différentiel et fonctions holomorphes
- Densité des polynômes orthogonaux (, )
- Formule des compléments (, )
- Lemme de Borel (, )
- Lemme de Morse
- Méthode de Laplace (, )
- Méthode de Newton
- Surjectivité de l'exponentielle (, )
- Théorème de D'Alembert-Gauss ( ; )
- Théorème de Cartan-Von Neumann (, )
- Théorème des extrema liés
- Théorème de Montel
Équations différentielles
- Solution élémentaire de l'équation de Schrodinger
- Théorème de Cauchy-Arzela-Peano (, )
- Théorème de stabilité de Lyapounov
- Théorème de Cauchy-Lipschitz
Intégration
- Critère de Weyl (, )
- Un exemple de calcul d'intégrale (, )
- Formule sommatoire d'Euler Maclaurin
- Formule Sommatoire de Poisson
- Formule des compléments (, )
- Formule d'inversion de Fourier
- Intégrale de Fresnel
- Méthode de Gauss d'approximation d'intégrale (, )
- Méthode de Laplace (, )
- Prolongement de la fonction
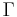(, ) - Théorème d'Abel angulaire (, )
- Théorèmes d'Abel angulaire et taubérien faible
- Théorème de Fejér
Probabilités
- Autour des variables aléatoires gaussiennes (, )
- Bernoulli et développement dyadique
- Marche aléatoire sur Z
- Ruine du joueur (, )
- Théorème central limite (, )
- Théorème de Weierstrass via les probabilités : ,)
Topologie
- Ellipsoïde de John-Lœwner
- Composantes connexes de l'ensemble des formes quadratiques non dégénérées.
- Lemme de Morse
- Sous-groupes compacts de
- Théorème de Banach-Steinhaus et application aux séries de Fourier
- Théorème de Brouwer en dimension 2 (, )
- Théorème de Cartan Von Neumann
- Théorème de Fejér
- Théorème de Jordan (, )
- Théorème de Montel
- Théorème de Müntz
- Le théorème de Weierstrass (via les polynômes de Bernstein)
Non classés
Informatique
Algorithmique et structures de données
- 2SAT est décidable en temps linéaire
- Arbres binaires de recherche optimaux
- Automate des occurrences
- Hachage parfait
- Plus longue sous-séquence commune
- Algorithme d'unification
Complexité
- 2SAT est décidable en temps linéaire
- Problème de séparation par automates
- Universalité d'un langage rationnel
- Théorème de Cook
Décidabilité
Langages formels
- Automate des occurrences
- Arithmétique de Presburger ( ; )
- Langage de pile d'un automate à pile ( ; )
- Problème de séparation par automates
- Universalité d'un langage rationnel
Logique
- Arithmétique de Presburger ( ; )
- Fonction d'Ackermann
- Algorithme d'unification
- Complétude de la méthode de résolution
- Exemple d'un programme PROLOG
