Formule d'inversion de Fourier

Recasage :

• 234 -- Espaces L^p, 1 ≤ p ≤ +∞. (version dans $L^{1}({\mathbb R})$)
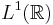• 235 -- Suites et séries de fonctions intégrables. Exemples et applications. (version avec les approximations de l'unité)
• 236 -- Illustrer par des exemples quelques méthodes de calculs d'intégrales de fonctions d'une ou plusieurs variables réelles. (version avec la transformée de la gaussienne)
• 239 -- Fonctions définies par une intégrale dépendant d'un paramètre. Exemples et applications.
• 240 -- Produit de convolution, transformation de Fourier. Applications.
• 241 -- Suites et séries de fonctions. Exemples et contre-exemples. (version avec les approximations de l'unité)
• 247 -- Exemples de problèmes d'interversion de limites.
• 254 -- Espaces de Schwartz S(R^d) et distributions tempérées. Transformation de Fourier dans S(R^d) et S'(R^d). (version dans ${\mathcal S}({\mathbb R})$)
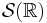• 255 -- Espaces de Schwartz. Distributions. Dérivation au sens des distributions. (version dans ${\mathcal S}({\mathbb R})$)

• Version dans ${\mathcal S}({\mathbb R})$ :

• Version dans $L^{1}({\mathbb R})$ avec les approximations de l'unité : ,

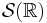On remarque en fait a posteriori que la version dans 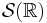${\mathcal S}({\mathbb R})$ n'est pas plus faible que celle dans 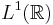$L^{1}({\mathbb R})$ (une fois qu'on a cette deuxième version). En effet, dans la version 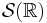${\mathcal S}({\mathbb R})$, les seules hypothèses sur 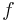$f$ qu'on utilise est son intégrabilité, sa continuité et son caractère borné (ces deux dernières hypothèses sont nécessaires pour appliquer le théorème de convergence dominée à la fin). 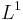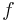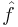Or la transformée de Fourier d'une fonction $L^{1}$ est justement continue et bornée donc, en appliquant la formule d'inversion, on remarque que si $f$ et ${\hat f}$ sont dans 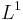$L^{1}$, alors 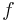$f$ est continue (presque partout) et bornée. On ne perd donc rien à supposer au départ que 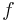$f$ est continue et bornée.