909 -- Langages rationnels. Exemples et applications.

Plan de Kévin et Basile (2012)

Le Plan

I) Expressions Rationnelles

1. Définitions
   • Par induction
   • Par récurrence et hauteur
2. Sémantique
   • Interprétation
   • Exemples
   • Hauteur d'étoile (généralisé ... bof)
   • Langage de hauteur d'étoile $n$
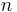
3. Équations
   • Lemme d'ARDEN
   • Pivot de GAUSS
4. Réduction des expressions rationnelles
   • Décidabilité de l'équivalence
   • Exemple
   • Le problème d'universalité est PSPACE-Complet (DEV)
5. Ordre sous-mot
   • Définition, de l'ordre, des antichaînes (ensemble d'éléments incomparables deux à deux )
   • Théorème de Higman et ses corollaires ( les sous-mots et les sur-mots d'un langage sont rationnels )

II) Caractérisations

1. Théorème de Kleene
   • Dérivées d'Antimirov et résolutions d'équations par le lemme d'Arden
2. Lemme de l'étoile [Carton p. 54]
   • version par bloc
   • Théorème (EPR) : Caractérisation par le lemme de l'étoile par blocs appliqué au langage et à son complémentaire.
3. Grammaire régulières
   • Caractérisation par les langages de grammaires linéaires gauches.
4. Automate à Pile
   • Définition langage de Dyck et langage de Pile
   • Le langage de Pile d'un automate à pile est reconnaissable (DEV)
5. Reconnaissance par monoïde
   • Définition
   • Théorème de caractérisation : reconnaissance par monoïde fini.
   • Exemple
   • Propriétés de stabilité par morphismes
6. Théorème de Myhill-Nérode [Carton p. 45]
   • Définition résiduels
   • Exemples
   • Caractérisation par finitude du nombre de résiduels

III) Cas d'un monoïde quelconque [Carton p. 72]

1. Définitions : Reconnaissance par monoïde fini, Rationalité...
2. Version faible du théorème de Kleene.
   • Exemples et contre-exemples

IV) Applications

1. Analyse Lexicale.
   • Expressions régulières
   • Exemples de commandes...
   • Application à la compilation

Développements possibles

1. Le problème d'universalité d'un langage rationnel est PSPACE-dur
   • Le caractère PSPACE est admis pour des raisons de temps.
2. Langage de Pile d'un Automate à Pile ( Source .tex ; .pdf)

1. Caractérisation de la rationalité par le lemme de l'étoile par blocs (immonde)
2. Théorème de Higman et corollaires :
   • Il n'existe pas d'antichaïne infinie pour l'ordre lexicographique sur le monoïde libre d'un alphabet fini.
   • Les surmots et sousmots pour l'ordre lexicographique d'un langage quelconque sont rationnels.
3. (Presburger)
4. (Séparation par automate)
   • Montré indécidable par réduction à 3-SAT

Références

Carton... "C'est mal de ne pas mettre quelque chose qui est dans le Carton, c'est mal de mettre quelque chose qui n'est pas dans le Carton." (D. Cachera)