246 -- Séries de Fourier. Exemples et applications.
De AgregmathKL
Révision de 1 décembre 2011 à 16:03 par Basile (discuter | contributions) (pré-création de la page en prévision du jours où je commencerai à bosser cette leçon)
"Les différents modes de convergence (L 2 , Fejer, Dirichlet
etc...) doivent être connus. Il faut avoir les idées claires sur la notion de fonctions de classe 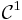 par
morceaux (elles ne sont pas forcément continues). Dans le cas d’une fonction continue et
par
morceaux (elles ne sont pas forcément continues). Dans le cas d’une fonction continue et 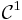 par
morceaux on peut conclure sur la convergence normale de la série Fourier sans utiliser le théorème
de Dirichlet. Cette leçon ne doit pas se réduire à un cours abstrait sur les coefficients de Fourier."
par
morceaux on peut conclure sur la convergence normale de la série Fourier sans utiliser le théorème
de Dirichlet. Cette leçon ne doit pas se réduire à un cours abstrait sur les coefficients de Fourier."
Extrait du rapport du jury 2010.