908 -- Automates Finis, exemples et applications
De AgregmathKL
Révision de 21 avril 2022 à 21:20 par Antoine De (discuter | contributions)
Sommaire
Plan d'Emmanuel et Ivan (2012)
Le Plan
On se place sur un alphabet fini 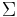 .
.
I - Automates finis et langages reconnaissables
I.1 - Définitions et Propriétés
- Définitions : Automates finis, calcul/chemin, mots acceptés, langages reconnu par un AF,
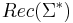 , AF complet, émondé, à epsilon transitions, déterministe.
, AF complet, émondé, à epsilon transitions, déterministe. - Thm : tout AF peut etre émondé, complété, déterminisé, desespsilonisé.
- Exemples de chaque type et leurs images par le théorème.
- Remarque : tout déterminisé d'un AF a au plus
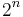 états.
états.
- Prop : Problème du vide et problème du mot sont décidables
- Complexité en
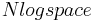 .
.
- Complexité en
I.2 - Propriétés de clôtures et lemme d'itération
- Lemme de l'étoile
- Propriétés de clôture de
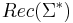
II - Langages Rationnels
- Déf :
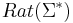
- Thm de Kleen
- exemples :
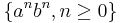
III - Automate minimal
But : 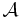 AF, trouver
AF, trouver 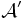 AFDC de même langage et minimal pour le nombre d'état
AFDC de même langage et minimal pour le nombre d'état
- Déf et prop sur les quotients à gauches
- Déf, prop classiques
- Thm : l'automate minimal est l'automate des quotients
- Prop : caract des langages rationnels par la finitude de l'ensemble des quotients à gauche
- Congruence de Nérode
- Déf congruence
- Déf congruence de Nérode
- Prop : l'algo de Moore calcule la congruence de Nérode en
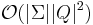 .
.
IV - Applications ...
IV.1 - ... à la logique
- Thm de Presburger [Dev 1]
IV.2 - ... à l'analyse lexicale
- Définir les notions et insister sur la place de l'analyse lexicale dans la chaîne de compilation
- Exemple si la place
IV.3 - à l'algorithmique du texte
- Algo naïf de recherche d'un mot dans un texte + complexité
- Algo par automate + complexité
- Algo Morris et Pratt + complexité
- Conclure sur le fait que les automates sont pas trop mal pour ce type de problème.
IV.4 - ... à la classification
- Déf de la séparation de deux langages par un automate (PSA)
- PSA est NP-Complet [Dev 2]
Développements possibles
- Thm de Presburger [Carton] - se place dans les leçons [908], [909] (moins), [914], [924]
- PSA est NP-Complet [Sakarovitch] - se place dans les leçons [908], [915]
- Thm de Kleen - se place dans les leçons [908], [909], autre ? - développement très peu innovant, les jury ne l'aiment pas.
- Congruence de Nérode
- Knuth-Morris-Pratt - je ne garanti pas qu'il soit faisable en développement mais si oui il se recase en algo du texte, et complexité.
Références
- Luc Albert - pour la quasi totalité du plan
- Carton - pour Presburger et compléments du plan
- Sakarovitch - Pour PSA est NP-complet - pas très lisible pour faire un plan
- David, Nour, Raffalli - Introduction à la logique - Pour les bases de la logique pour Presburger (pour les questions qui viendrons après)