149 -- Groupes finis de petit cardinal.

Plan

L'objet du plan est de donner les théorèmes et les définitions qui permettent d'étudier les groupes de petits cardinaux.

1) Préliminaires

2) Action d'un groupe sur un ensemble, formule des classes, produit semi-direct

3) Sylow

4) Classification des groupes d'ordre inférieur à 15

Développements

Groupes d'ordre 12, groupes d'ordre 8, simplicité de 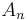$A_{n}$

Je fais ici le développement que Guirardel nous avait proposé et qu'on n'a pas mis dans le plan.

Théorème : Pour n différent de 6, $Aut(S_{n})=Int(S_{n})$

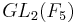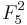On considère l'action de $GL_{2}(F_{5})$ sur $F_{5}^{2}$. Cette action est transitive.

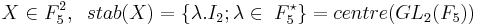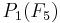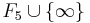Pour $X\in F_{5}^{2},\;\;stab(X)=\{\lambda .I_{2};\lambda \in \;F_{5}^{\star }\}=centre(GL_{2}(F_{5}))$. On identifie maintenant la droite projective $P_{1}(F_{5})$ à $F_{5}\cup \{\infty \}$ et on pose 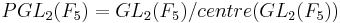$PGL_{2}(F_{5})=GL_{2}(F_{5})/centre(GL_{2}(F_{5}))$. L'action définie précédemment livre (par définition d'une action de groupe) un morphisme 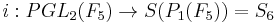$i:PGL_{2}(F_{5})\to S(P_{1}(F_{5}))=S_{6}$. Ce morphisme est injectif car l'action est fidèle.

Ainsi, on a vu que 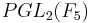$PGL_{2}(F_{5})$ s'injecte dans $S_{6}$.

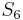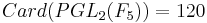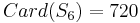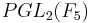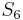De plus, $Card(PGL_{2}(F_{5}))=120$ et $Card(S_{6})=720$ donc si K est l'image de $PGL_{2}(F_{5})$ dans $S_{6}$, on a que K est d'indice 6.

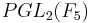De plus, on sait que l'action de K ne fixe aucun point de $\{1,\dots ,6\}$ car $PGL_{2}(F_{5})$ ne fixe aucun point de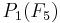 $P_{1}(F_{5})$

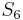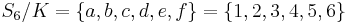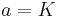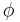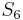Enfin, $S_{6}$ agit sur $S_{6}/K=\{a,b,c,d,e,f\}=\{1,2,3,4,5,6\}$ par translations à gauche (où on a posé $a=K$ puis on envoie a sur 1, b sur 2,etc). Cette action livre un automorphisme $\phi$ de $S_{6}$ qui est tel que $\phi (K)=S(\{2,3,4,5,6\})\cong S_{5}$.

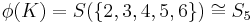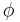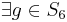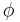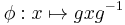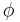Si $\phi$ est intérieur, $\exists g\in S_{6}$ tel que $\phi$ s'écrit $\phi :x\mapsto gxg^{{-1}}$ et alors $\phi (stab(1point))=stab(g(cepoint))$ et donc $\phi$ établit une bijection entre les sous-groupes d'indice 6 qui fixent un point. Ce qui contredit le fait que 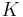$K$ ne fixe aucun point et 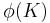$\phi (K)$ fixe 1.

Rapport de Jury

Groupes finis de petit cardinal. Après avoir cité rapidement les théorèmes fondamentaux sur les groupes, la leçon doit se concentrer sur les exemples. Les développements ne peuvent pas porter sur les théorèmes généraux. C’est une leçon bien distincte de la leçon Groupes finis.

Références

Perrin Querré cours d'algèbre Gourdon algèbre Tauvel Mathématiques générales pour l'agrégation Francinou, Gianella exercices de mathématiques pour l'agrégation Algèbre 1