Théorème de Molien
On étudie dans ce développement une action d'un sous-groupe fini de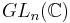 
sur les polynômes homogènes de degré k et on donne une relation sur la série génératrice des dimensions de l'espace des points fixes sous cette action.
Ce développement rentre très bien dans les leçons sur les représentations à condition d'adapter le vocabulaire. Le morphisme associé à l'action devient une représentation et les traces deviennent des caractères.
Attention à la démonstration de Leichtnam, elle contient un certain nombre d'erreurs.
En ce qui concerne Molien, étant d'origine lettone, son nom se prononce probablement à la lettone. Ce qui donne peu ou prou la même chose qu'une prononciation à l'anglaise.
Référence : Exercices d'oraux X-ENS : tome Algèbre et Géométrie, Eric Leichtnam.
Recasage :
- 101 -- Groupe opérant sur un ensemble. Exemples et applications.
- 104 -- Groupes finis. Exemples et applications.
- 107 -- Représentations et caractères d'un groupe fini sur un C-espace vectoriel.
- 117 -- Algèbre des polynômes à n indéterminées (n ≥ 2). Polynômes symétriques. Applications.
- 120 -- Dimension d'un espace vectoriel (on se limitera au cas de la dimension finie). Rang. Exemples et applications.
- 125 -- Sous-espaces stables d'un endomorphisme d'un espace vectoriel de dimension finie. Applications.
- 145 -- Méthodes combinatoires, problèmes de dénombrement.
- 149 -- Représentations de groupes finis de petit cardinal.
