183 -- Utilisation des groupes en géométrie. : Différence entre versions
m (cat) |
(→Développements envisageables) |
||
| Ligne 3 : | Ligne 3 : | ||
== Développements envisageables == | == Développements envisageables == | ||
| − | Classification des sous-groupes finis de SO(3). [[Média:Sous_groupes_finis_SO3.tex]] | + | *Classification des sous-groupes finis de SO(3). [[Média:Sous_groupes_finis_SO3.tex]] |
| − | + | *Action de <math>PSL_2(\mathbb Z)</math> sur le demi-plan de Poincaré (peut-être un peu court). | |
| − | Action de <math>PSL_2(\mathbb Z)</math> sur le demi-plan de Poincaré (peut-être un peu court). | + | *Action du groupe circulaire sur la droite projective complexe. [[Média:groupecirc.tex]] (attention il y a des images insérées dans le tex qui produiront une erreur puisqu'elles ne seront pas sur votre poste... à virer du code donc, ou vous pouvez me les demander (Laurent) ;)). |
| − | + | *[[Classification des groupes de pavage du plan]] | |
| − | Action du groupe circulaire sur la droite projective complexe. [[Média:groupecirc.tex]] (attention il y a des images insérées dans le tex qui produiront une erreur puisqu'elles ne seront pas sur votre poste... à virer du code donc, ou vous pouvez me les demander (Laurent) ;)). | + | |
Nota : pour le groupe circulaire, à trouver dans Audin : c'est là où c'est le mieux fait, mais malheureusement ça reste pas génial ! Notamment, il n'y a aucune démonstration concernant les figures obtenues une fois le point (ou la droite) envoyé à l'infini. Elle ne le mentionne pas, mais il faut donc impérativement adjoindre à l'apprentissage de ce développement, une lecture de la partie de géométrie plane sur les inversions (qui est pas mal faite dans le même livre), et, c'est mon avis mais il y a peut être mieux, voir l'homographie mise en jeu comme une composée d'inversion et de symétrie. Sans ça on peut pas vraiment justifier les figures, or elles sont fondamentales dans la démonstration... | Nota : pour le groupe circulaire, à trouver dans Audin : c'est là où c'est le mieux fait, mais malheureusement ça reste pas génial ! Notamment, il n'y a aucune démonstration concernant les figures obtenues une fois le point (ou la droite) envoyé à l'infini. Elle ne le mentionne pas, mais il faut donc impérativement adjoindre à l'apprentissage de ce développement, une lecture de la partie de géométrie plane sur les inversions (qui est pas mal faite dans le même livre), et, c'est mon avis mais il y a peut être mieux, voir l'homographie mise en jeu comme une composée d'inversion et de symétrie. Sans ça on peut pas vraiment justifier les figures, or elles sont fondamentales dans la démonstration... | ||
Version du 11 janvier 2013 à 22:00
Plan possible
Voici le plan que Laurent et moi (Gwenael) avons proposé Média:Plan_groupes_geometrie.tex. À noter, pour les références, l'excellent livre de Moulin, Ramis et Warusfel, et pour l'étude des polyèdres réguliers de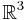 
, le poly d'Arnaudiès. C'est la seule référence qu'on ait trouvée qui ne suppose pas les polyèdres réguliers connus pour la classification.
Développements envisageables
- Classification des sous-groupes finis de SO(3). Média:Sous_groupes_finis_SO3.tex
- Action de
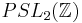sur le demi-plan de Poincaré (peut-être un peu court). - Action du groupe circulaire sur la droite projective complexe. Média:groupecirc.tex (attention il y a des images insérées dans le tex qui produiront une erreur puisqu'elles ne seront pas sur votre poste... à virer du code donc, ou vous pouvez me les demander (Laurent) ;)).
- Classification des groupes de pavage du plan
Nota : pour le groupe circulaire, à trouver dans Audin : c'est là où c'est le mieux fait, mais malheureusement ça reste pas génial ! Notamment, il n'y a aucune démonstration concernant les figures obtenues une fois le point (ou la droite) envoyé à l'infini. Elle ne le mentionne pas, mais il faut donc impérativement adjoindre à l'apprentissage de ce développement, une lecture de la partie de géométrie plane sur les inversions (qui est pas mal faite dans le même livre), et, c'est mon avis mais il y a peut être mieux, voir l'homographie mise en jeu comme une composée d'inversion et de symétrie. Sans ça on peut pas vraiment justifier les figures, or elles sont fondamentales dans la démonstration...
Références
Moulin, Ramis, Warufsel. Cours de mathématiques pures et appliquées - Volume 1 - Algèbre et géométrie.
J.-M. Arnaudiès. Les cinq polyèdres réguliers de 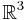et leurs groupes. Centre de Documentation Universitaire.
M. Audin. Géométrie.
M. Alessandri. Thèmes de géométrie.
P. Tauvel. Cours de géométrie.
Y. Ladegaillerie. Géométrie - Affine, projective, euclidienne et anallagmatique.
J.-P. Serre. Cours d'arithmétique.
