208 -- Espaces vectoriels normés, applications linéaires continues. Exemples. : Différence entre versions

De AgregmathKL
Aller à : navigation, rechercher
(Page créée avec « /!\ Page en travaux /!\ (Nil) ====Définir un espace vectoriel normé ?==== Dans [N. Bourbaki, Topologie Générale, IX, p. 29] on apprend qu'il suffit que l'espace vectorie... »)
 
Ligne 1 : Ligne 1 :
−
/!\ Page en travaux /!\ (Nil)
+
Quelques remarques qui me paraissent pertinentes : (Nil)
  
 
====Définir un espace vectoriel normé ?====
 
====Définir un espace vectoriel normé ?====
Ligne 5 : Ligne 5 :
  
 
====Situer les EVN dans le paysage topologique====
 
====Situer les EVN dans le paysage topologique====
−
La norme est une manière simple de répondre à la question : "Comment fabriquer une topologie sur un EV qui rende continues les opérations ?". Tout Espace vectoriel sur un corps muni d'une valeur absolu peut être muni d'une norme. (Voir une idée de preuve donnée par Christophe Cheverry) Pour autant, toute topologie d'espace vectoriel n'est pas issue d'une norme. En contre-exemple, on peut penser, par décroissance de risque à mon avis, à de la topologie faible et à de la topologie d'espace vectoriel localement convexe (Issue d'une famille de semi-normes, en particulier pas forcément séparée : c'est peut être pas mal puisque les distributions sont au programme maintenant.) L'exemple le moins dangereux qu'on ait trouvé est <math>\mathcal L^p</math> muni de sa semi-norme, qui n'est pas séparé.
+
La norme est une manière simple de répondre à la question : "Comment fabriquer une topologie sur un EV qui rende continues les opérations ?". Tout Espace vectoriel sur un corps muni d'une valeur absolu peut être muni d'une norme (Voici une idée de preuve donnée par Christophe Cheverry : Tout Espace vectoriel <math>E</math> admet une base algébrique <math>(b_i)_{i \in I}</math>, d'où <math>\forall x \in E, \exists J \subset I</math> fini tel que  <math> x=\sum_{i \in J}x_i b_i </math>. On pose alors <math>\|x\|=max(x_i)</math> ). Pour autant, toute topologie d'espace vectoriel n'est pas issue d'une norme. En contre-exemple, on peut penser, par décroissance de risque à mon avis, à de la topologie faible et à de la topologie d'espace vectoriel localement convexe (Issue d'une famille de semi-normes, en particulier pas forcément séparée : c'est peut être pas mal puisque les distributions sont au programme maintenant.) L'exemple le moins dangereux qu'on ait trouvé est <math>\mathcal L^p</math> muni de sa semi-norme, qui n'est pas séparé.
−
 
+
−
====A propos de la notion de normes équivalentes====
+

Version du 13 novembre 2010 à 22:10

Quelques remarques qui me paraissent pertinentes : (Nil)

Définir un espace vectoriel normé ?

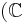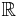Dans [N. Bourbaki, Topologie Générale, IX, p. 29] on apprend qu'il suffit que l'espace vectoriel soit sur un corps muni d'une valeur absolue pour définir une norme. C'est donc une notion qui s'étend au delà des ({\mathbb {C}} ou {\mathbb {R}})-espaces vectoriels. Par exemple, on peut définir des 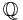{\mathbb Q}-espaces vectoriels normés, mais aussi des 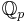{\mathbb {Q}}_{p}-espaces vectoriels normés, où les 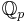{\mathbb {Q}}_{p} désignent les corps p-adiques : définir les EVN avec cette généralité me paraît donc tout à fait dangereux. 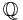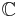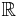En revanche, parler de {\mathbb Q}-espaces vectoriels normés permet d'éclairer certains résultats, qui sont vrais sur {\mathbb {C}} ou {\mathbb {R}} mais pas sur 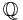{\mathbb Q}, parce que la complétude interviens dans la preuve. (En dimension finie : La complétude bien sûr, mais aussi l'équivalence de toutes les normes, et probablement également la continuité automatique des applications linéaires (à vérifier)).

Situer les EVN dans le paysage topologique

La norme est une manière simple de répondre à la question : "Comment fabriquer une topologie sur un EV qui rende continues les opérations ?". Tout Espace vectoriel sur un corps muni d'une valeur absolu peut être muni d'une norme (Voici une idée de preuve donnée par Christophe Cheverry : Tout Espace vectoriel 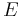E admet une base algébrique 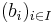(b_{i})_{{i\in I}}, d'où 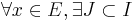\forall x\in E,\exists J\subset I fini tel que 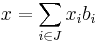x=\sum _{{i\in J}}x_{i}b_{i}. On pose alors 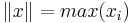\|x\|=max(x_{i}) ). Pour autant, toute topologie d'espace vectoriel n'est pas issue d'une norme. En contre-exemple, on peut penser, par décroissance de risque à mon avis, à de la topologie faible et à de la topologie d'espace vectoriel localement convexe (Issue d'une famille de semi-normes, en particulier pas forcément séparée : c'est peut être pas mal puisque les distributions sont au programme maintenant.) L'exemple le moins dangereux qu'on ait trouvé est 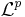{\mathcal L}^{p} muni de sa semi-norme, qui n'est pas séparé.

Récupérée de « https://minerve.ens-rennes.fr/index.php?title=208_--_Espaces_vectoriels_normés,_applications_linéaires_continues._Exemples.&oldid=50 »