229 -- Fonctions monotones. Fonctions convexes. Exemples et applications. : Différence entre versions
(Page créée avec « Dans la liste des développements pour la leçon 229, il y a ceux qu'Antoine Marnat et moi-même (Simon Billouet) avons proposé : ellipsoïde de John-Löwner (développement... ») |
(Aucune différence)
|
Version du 25 octobre 2010 à 20:49
Dans la liste des développements pour la leçon 229, il y a ceux qu'Antoine Marnat et moi-même (Simon Billouet) avons proposé : ellipsoïde de John-Löwner (développement qui se recase dans plein de leçons, et pour être honnête on l'avait mis pour avoir un troisième développement...) ; théorème des trois droites d'Hadamard (que je trouve à la limite du hors-sujet, il faut en tout cas être très à l'aise sur l'holomorphie et particulièrement le principe du maximum pour le présenter) ; théorème de Helly et théorème de Dini.
Pour ceux qui trouvent que l'alliance "Helly/Dini" est artificielle, je suis d'accord. Une solution trouvée pour les fans de probas peut être trouvée en mettant un "Helly/Prokorov". Le théorème de Prokorov est une application de Helly qui dit qu'une suite de probabilités tendues sur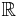 
(i.e.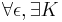 
compact tel que 
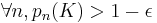) admet une sous-suite qui converge étroitement. Je ne ferai pas ce choix mais bon...
Enfin, un développement qui rentrerait plus dans la leçon est de développer la méthode du gradient (on peut même prendre un exemple si on est trop court). L'intérêt est que ça se recase aussi dans des leçons type "Convergence des suites numériques" pour des raisons que je n'expliciterai pas. LA référence sur le sujet est le bouquin de Ciarlet "Introduction à l'analyse numérique matricielle et à l'optimisation".
