240 -- Produit de convolution, transformation de Fourier. Applications. : Différence entre versions
De AgregmathKL
| (9 révisions intermédiaires par 6 utilisateurs non affichées) | |||
| Ligne 32 : | Ligne 32 : | ||
Rien de bien original, certes. | Rien de bien original, certes. | ||
| + | |||
| + | == Autres plans == | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:240_2013-2014.pdf | Plan scanné de l'année 2013-2014]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:240_2014-2015.pdf | Plan scanné de l'année 2014-2015]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:240_2015-2016.pdf | Plan scanné de l'année 2015-2016]] | ||
| + | |||
| + | == La nouvelle leçon qui la remplace en 2016-2017 == | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:250_2016-2017.pdf | Plan scanné de l'année 2016-2017]] | ||
| + | |||
| + | [[Category:Anciennes leçons]] | ||
Version du 27 août 2021 à 21:48
Selon Laurent Guillopé (jury aux oraux blancs), il faut savoir calculer la transformée de Fourier :
- d'une fonction constante ;
- d'une fonction créneau (fontion caractéristique de
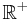 ) : cela donne l'exemple d'une fonction analytique non
) : cela donne l'exemple d'une fonction analytique non 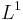 ;
; - de la Gaussienne ;
- de
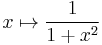 ;
; - de
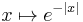 (ces deux dernières étant reliées).
(ces deux dernières étant reliées).
Voici le plan que j'envisage:
- I Convolution
- i)Définitions
Le cas général d'existence semble porter le nom de théorème de Young.
- ii)Régulariastion et approximation
On énonce un théorème qui dit que la convolée garde la régularité de la fonction la plus régulière. Approximations de l'unité. Théorèmes de densité.
- II Transformation de Fourier
- i)Dans
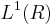 , lien avec la convolution. Formule sommatoire de Poisson
, lien avec la convolution. Formule sommatoire de Poisson - ii)Dans l'espace de Schwartz, inversion, prolongement à
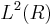
- iii)Application à l'équation de la chaleur
- III Extension de la transformation de Fourier aux distributions tempérées
- i)Définition de l'espace
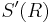
- ii)Transformation de Fourier dans
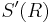 , applications à la résolution d'une EDP
, applications à la résolution d'une EDP
Rien de bien original, certes.
Autres plans
![]() Plan scanné de l'année 2013-2014
Plan scanné de l'année 2013-2014
![]() Plan scanné de l'année 2014-2015
Plan scanné de l'année 2014-2015
![]() Plan scanné de l'année 2015-2016
Plan scanné de l'année 2015-2016