120 -- Anneaux Z/nZ. Applications. : Différence entre versions
De AgregmathKL
m (Catégorification) |
|||
| Ligne 1 : | Ligne 1 : | ||
On peut trouver des "équations diophantiennes bien choisies" dans '' Arithmétique'' de Marc Hindry avec notamment le nombre de racines m-ième dans l'anneau. On y trouve également des tests de primalité et le système RSA pour ceux que ça intéresse. | On peut trouver des "équations diophantiennes bien choisies" dans '' Arithmétique'' de Marc Hindry avec notamment le nombre de racines m-ième dans l'anneau. On y trouve également des tests de primalité et le système RSA pour ceux que ça intéresse. | ||
| + | |||
| + | == Plan de Hugo et Thibault (2012) == | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Anneaux Z sur nZ.pdf | Plan 2012]] | ||
| + | |||
| + | == Développements == | ||
| + | * Groupes d'ordre <math>pq</math> | ||
| + | * Irréductibilité des polynômes cyclotomiques sur <math>\mathbb Z [X]</math> | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Développements.pdf | Groupes d'ordre <math>pq</math> et polynômes cyclotoniques]] | ||
| + | |||
[[Category:Leçon de l'option D]] | [[Category:Leçon de l'option D]] | ||
Version du 16 avril 2012 à 22:40
On peut trouver des "équations diophantiennes bien choisies" dans Arithmétique de Marc Hindry avec notamment le nombre de racines m-ième dans l'anneau. On y trouve également des tests de primalité et le système RSA pour ceux que ça intéresse.
Plan de Hugo et Thibault (2012)
Développements
- Groupes d'ordre
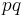
- Irréductibilité des polynômes cyclotomiques sur
![{\mathbb Z}[X]](/images/math/e/f/6/ef616d0b1baef82f69bc42b50836f19a.png)