Exos classiques et autres démonstrations : Différence entre versions
De AgregmathKL
(Page créée avec « = Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage = Soit <math> A \in \mathcal{M}_n(\mathbb{C}) </math>... ») |
(→Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage) |
||
| Ligne 1 : | Ligne 1 : | ||
= Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage = | = Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage = | ||
| − | Soit <math> A \in \mathcal{M}_n(\mathbb{C}) </math>... | + | Soit <math>A \in \mathcal{M}_n(\mathbb{C})</math>. |
| + | soit <math>D=diag(\lambda_1,\dots,\lambda_n)</math> telle que <math>A=Q^{-1}DQ</math>. | ||
| + | Soit <math>P</math> un polynôme tel que <math>P(\lambda_i) = e^{\lambda_i}</math> pour tout <math>i</math>. | ||
| + | Alors <math>P(A) = P(Q^{-1}DQ) = Q^{-1}P(D)Q = Q^{-1}\exp(D)Q = \exp(A)</math> ! | ||
Version du 21 juin 2013 à 10:39
Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage
Soit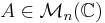 
.
soit 
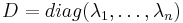telle que 
.
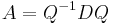Soit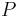 
un polynôme tel que 
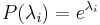pour tout 
.
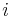Alors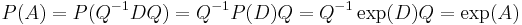 
!
