Exos classiques et autres démonstrations
Sommaire
- 1 Algèbre
- 1.1 Calcul des projecteurs sur les sous-espaces caractéristiques d'un endomorphisme
- 1.2 Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage
- 1.3 Expression d'un polynôme symétrique en fonction des polynômes symétriques élémentaires
- 1.4 Le groupe multiplicatif d'un corps fini est cyclique
- 1.5 Méthode de Gauss pour les formes quadratiques
- 1.6 Pseudo-réduction simultanée
- 1.7 Racine carrée d'une matrice symétrique réelle positive
- 1.8 Une famille d'endomorphismes diagonalisables qui commutent est codiagonalisable
- 2 Analyse
- 2.1 Ind est une fonction à valeurs entières, constante sur chaque composante connexe
- 2.2 L'espace de Schwartz sur est stable par transformée de Fourier
- 2.3 Lemme de Baire
- 2.4 Lemme de Riemann-Lebesgue
- 2.5 Limite uniforme de polynômes
- 2.6 Théorème de Cauchy-Peano
- 2.7 Théorème d'inversion locale
- 2.8 Théorème de représentation de Riesz
- 2.9 Théorème des fonctions implicites
Algèbre
Calcul des projecteurs sur les sous-espaces caractéristiques d'un endomorphisme
On donne ici une méthode pour calculer les projecteurs sur les sous-espaces caractéristiques d'un endomorphismes, ainsi qu'une application au calcul de l'exponentielle matricielle par la décomposition de Dunford.
Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage
Soit 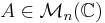 .
soit
.
soit 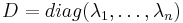 telle que
telle que 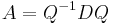 .
.
Soit 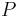 un polynôme tel que
un polynôme tel que 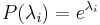 pour tout
pour tout 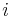 .
.
Alors 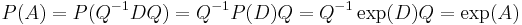 !
!
Ref : perso.univ-rennes1.fr/tristan.vaccon/exponentielle_de_matrices.pdf
Expression d'un polynôme symétrique en fonction des polynômes symétriques élémentaires
Le groupe multiplicatif d'un corps fini est cyclique
Méthode de Gauss pour les formes quadratiques
Pseudo-réduction simultanée
Racine carrée d'une matrice symétrique réelle positive
Une famille d'endomorphismes diagonalisables qui commutent est codiagonalisable
Analyse
Ind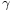 est une fonction à valeurs entières, constante sur chaque composante connexe
est une fonction à valeurs entières, constante sur chaque composante connexe
L'espace de Schwartz sur 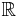 est stable par transformée de Fourier
est stable par transformée de Fourier
Lemme de Baire
Lemme de Riemann-Lebesgue
Limite uniforme de polynômes
Montrons que si une fonction 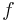 est limite uniforme d'une suite de polynômes
est limite uniforme d'une suite de polynômes 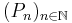 , alors
, alors 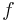 est un polynôme.
est un polynôme.
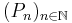 est une suite de Cauchy donc il existe
est une suite de Cauchy donc il existe 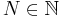 tel que pour tout
tel que pour tout 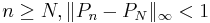 . Or
. Or 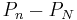 est un polynôme borné, donc est constant, on a
est un polynôme borné, donc est constant, on a 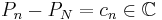 . Or
. Or 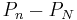 converge vers
converge vers 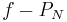 donc
donc 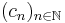 converge vers une constante
converge vers une constante 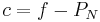 . D'où
. D'où 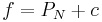 est un polynôme.
est un polynôme.
Référence : Xavier Gourdon, Analyse, Ellipses, 1994, p.228.
Théorème de Cauchy-Peano
On prouve ici le théorème de Cauchy-Peano en utilisant le théorème de point fixe de Schauder et le théorème d'Ascoli.