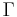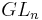Développements : Différence entre versions
(→Développements mixtes) |
m (Remplacement de texte — « \|24px » par « |24px ») |
||
| (73 révisions intermédiaires par 7 utilisateurs non affichées) | |||
| Ligne 5 : | Ligne 5 : | ||
== Développements d'algèbre == | == Développements d'algèbre == | ||
| − | |||
| − | [[ | + | * Automorphismes de <math>\mathbb{Z}/n\mathbb{Z}</math> ([[Fichier:Tex.png|alt=Tex|link={{filepath:AutomorphismesdeZnZ.tex}} |24px]]) |
| − | [[ | + | * Commutant d'un endomorphisme ([[Fichier:Tex.png|alt=Tex|link={{filepath:Commutant.tex}} |24px]]) |
| − | [[ | + | * [[Décomposition de Bruhat]] |
| − | [[ | + | * [[Décomposition de Dunford]] |
| − | [[ | + | * Ellipse de Steiner ([[Fichier:Tex.png|alt=Tex|link={{filepath:Ellipse_Steiner.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: Ellipse_Steiner.pdf}} |24px]]) |
| − | [[ | + | * Groupe circulaire ([[Fichier:Tex.png|alt=Tex|link={{filepath:Groupe_circulaire.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: Groupe_circulaire.pdf}} |24px]]) |
| − | [[ | + | * Groupes d'ordre 12 ([[Fichier:Tex.png|alt=Tex|link={{filepath:Groupe_d_ordre_douze.tex}} |24px]]) |
| − | [[ | + | * Irréductibilité des polynômes cyclotomiques ([[Fichier:Pdf.png|alt=Tex|link={{filepath: Cyclo.pdf}} |24px]]) |
| − | [[ | + | * [[Le paradoxe de Banach-Tarski]] |
| − | [[ | + | * Orthodiagonalisation des endomorphismes auto-adjoints ([[Fichier:Tex.png|alt=Tex|link={{filepath:Orthodiag.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: Orthodiag.pdf}} |24px]]) |
| − | [[ | + | * Polynômes irréductibles sur <math>\mathbb{F}_q</math> ([[Fichier:Tex.png|alt=Tex|link={{filepath:DenombrementpolyirreFq.tex}} |24px]]) |
| − | [[ | + | * Réduction des matrices normales ([[Fichier:Tex.png|alt=Tex|link={{filepath:Matrices_normales.tex}} |24px]]) |
| − | [[ | + | * Simplicité de <math>\mathfrak{A}_n</math> ([[Fichier:Tex.png|alt=Tex|link={{filepath:Simplicité_An.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: Simplicité.pdf}} |24px]]) |
| − | [[ | + | * Sous groupes finis de <math>\mathcal{SO}(3)</math> ([[Fichier:Tex.png|alt=Tex|link={{filepath:Sous_groupes_finis_SO3.tex}} |24px]]) |
| + | |||
| + | * [[Théorème de Burnside]] | ||
| + | |||
| + | * Théorème de Caratheodory ([[Fichier:Tex.png|alt=Tex|link={{filepath:Caratheodory.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: Caratheodory.pdf}} |24px]]) | ||
| + | |||
| + | * Théorème de Cartan-Dieudonné ([[Fichier:Tex.png|alt=Tex|link={{filepath:cartan_dieudonne.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: cartan_dieudonne.pdf}} |24px]]) | ||
| + | |||
| + | * [[Théorème de Hahn-Banach en dimension finie]] | ||
| + | |||
| + | * Théorème de Kronecker ([[Fichier:Tex.png|alt=Tex|link={{filepath:Kronecker.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: Kronecker.pdf}} |24px]]) | ||
| + | |||
| + | * Théorème de l'élément primitif ([[Fichier:Tex.png|alt=Tex|link={{filepath:element_primitif.tex}} |24px]]) | ||
| + | |||
| + | * Théorème de Sylow ([[Fichier:Tex.png|alt=Tex|link={{filepath:Sylow.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: Sylow.pdf}} |24px]]) | ||
| + | |||
| + | * Théorème de Wedderburn ([[Fichier:Pdf.png|alt=Tex|link={{filepath: Wedderburn.pdf}} |24px]]) | ||
| + | |||
| + | * Une version faible du théorème de Dirichlet ([[Fichier:Tex.png|alt=Tex|link={{filepath:Dirichlet_faible.tex}} |24px]]) | ||
| + | |||
| + | * [[Isomorphisme entre M_n(K) et son dual]] | ||
| + | |||
| + | * [[Probabilité que deux entiers soient premiers entre eux]] | ||
== Développements d'analyse == | == Développements d'analyse == | ||
| − | [[Média:MethodedeLaplace.tex | Méthode de Laplace]] | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:MethodedeLaplace.tex | Méthode de Laplace]] |
| − | [[Média:ProlongementGamma.tex | Prolongement de la fonction <math>\Gamma</math>]] | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:ProlongementGamma.tex | Prolongement de la fonction <math>\Gamma</math>]] |
| − | [[Média:devdyadique.tex | Bernoulli et développement dyadique]] | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:devdyadique.tex | Bernoulli et développement dyadique]] |
| − | [[ | + | Ruine du joueur ([[Fichier:Tex.png|alt=Tex|link={{filepath: Ruinedujoueur.tex}} |24px]], [[Fichier:Pdf.png|alt=Pdf|link={{filepath: Ruine.pdf}} |24px]]) |
| − | [[Média: | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:weierstrass.tex | Le théorème de Weierstrass (via les polynômes de Bernstein)]] |
| − | [[ | + | -> Le même résultat en passant par les probabilités : ([[Fichier:Tex.png|alt=Tex|link={{filepath: Bernstein_proba.tex}} |24px]], [[Fichier:Pdf.png|alt=Tex|link={{filepath: Bersntein_proba.pdf}} |24px]]) |
| − | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:glaeser.tex | Le théorème de Glaeser]] | |
| − | [[ | + | Théorème de Brouwer en dimension 2 ([[Fichier:Tex.png|alt=Tex|link={{filepath: Brouwer.tex}} |24px]], [[Fichier:Pdf.png|alt=Pdf|link={{filepath: Brouwer.pdf}} |24px]]) |
| − | [[Média: | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Borel.tex | Lemme de Borel]] |
| − | [[Média: | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Abel_angulaire.tex | Théorème d'Abel angulaire]] |
| − | [[Média: | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Calcul_integrale.tex | Un exemple de calcul d'intégrale]] |
| − | [[Média: | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Cauchy_arzela_peano.tex | Théorème de Cauchy-Arzela-Peano]] |
| − | [[ | + | Critère de Weyl ([[Fichier:Tex.png|alt=Tex|link={{filepath: Critere_Weyl.tex}} |24px]], [[Fichier:Pdf.png|alt=Pdf|link={{filepath: Critere_Weyl.pdf}} |24px]]) |
| − | [[ | + | Théorème central limite ([[Fichier:Tex.png|alt=Tex|link={{filepath: TCL.tex}} |24px]], [[Fichier:Pdf.png|alt=Pdf|link={{filepath: TCL.pdf}} |24px]]) |
| − | [[ | + | Autour des variables aléatoires gaussiennes ([[Fichier:Tex.png|alt=Tex|link={{filepath: va_gaussiennes.tex}} |24px]], [[Fichier:Pdf.png|alt=Pdf|link={{filepath: va_gaussiennes.pdf}} |24px]]) |
| − | [[ | + | Projection dans un espace de Hilbert ([[Fichier:Tex.png|alt=Tex|link={{filepath: proj_hilbert.tex}} |24px]], [[Fichier:Pdf.png|alt=Pdf|link={{filepath: proj_hilbert.pdf}} |24px]]) |
| − | [[Média: | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Fonctions_lipschitziennes.tex | Dérivée des fonctions lipschitziennes]] |
| − | [[Média: | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Formule_complements.tex | Formule des compléments]] |
| − | [[Média:Methode_gauss.tex | Méthode de Gauss d'approximation d'intégrale]] | + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Methode_gauss.tex | Méthode de Gauss d'approximation d'intégrale]] |
| + | |||
| + | * [[Théorème de Hadamard-Lévy]] | ||
| + | |||
| + | * [[Théorème de stabilité de Lyapounov]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Abel.pdf | Théorèmes d'Abel angulaire et taubérien faible]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Poisson.pdf | Formule Sommatoire de Poisson]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Riesz-fischer.pdf | Théorème de Fischer - Riesz]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Montel.pdf | Théorème de Montel]] | ||
| + | |||
| + | * [[Théorème de Cauchy-Lipschitz]] | ||
| + | |||
| + | * [[Théorème de Fejér]] | ||
| + | |||
| + | * [[Théorème de Banach-Steinhaus et application aux séries de Fourier]] | ||
| + | |||
| + | * [[Méthode de Newton]] | ||
| + | |||
| + | * [[Solution elementaire de l'equation de Schrodinger | Solution élémentaire de l'équation de Schrodinger]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:E-Mcb.pdf | Formule sommatoire d'Euler Maclaurin]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Fourier.pdf | Formule d'inversion de Fourier]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Fourier.pdf | Estimation des grands écarts]] | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:H1.pdf | Un espace de Sobolev]] | ||
| + | |||
| + | * [[Intégrale de Fresnel]] | ||
== Développements mixtes == | == Développements mixtes == | ||
| − | [[Media:Lie-Kolchin.tex|Lie-Kolchin]] | + | * Convergence d'une suite de polygônes vers l'isobarycentre ([[Fichier:Tex.png|alt=Tex|link={{filepath: conv_polygones.tex}} |24px]], [[Fichier:Pdf.png|alt=Pdf|link={{filepath: conv_polygones.pdf}} |24px]]) |
| + | |||
| + | * Théorème de Jordan ([[Fichier:Tex.png|alt=Tex|link={{filepath: Jordan.tex}} |24px]], [[Fichier:Pdf.png|alt=Pdf|link={{filepath: Jordan.pdf}} |24px]]) | ||
| + | |||
| + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Media:Lie-Kolchin.tex|Lie-Kolchin]] | ||
| + | |||
| + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Media:exponentielle.tex|Surjectivité de l'exponentielle]] | ||
| + | |||
| + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Simplicité SO(3).tex | Simplicité de SO(3)]] | ||
| + | |||
| + | * [[Sous-groupes compacts de GL_n | Sous-groupes compacts de <math>GL_n</math>]] | ||
| + | |||
| + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Cartan_von_neumann.tex | Théorème de Cartan Von Neumann]] | ||
| + | |||
| + | [[Fichier:Tex.png|alt=Tex|link=|24px]] [[Média:Gradient_optimal.tex | Convergence de la méthode de gradient à pas optimal (+Kantorovitch)]] | ||
| + | |||
| + | * [[Théorème de Müntz]] | ||
| + | |||
| + | * [[Lemme de Morse]] | ||
| + | |||
| + | * [[Lemme_de_Morse | Composantes connexes de l'ensemble des formes quadratiques non dégénérées.]] | ||
| + | |||
| + | * [[Ellipsoïde de John-Lœwner]] | ||
| + | |||
| + | * [[Marche aléatoire sur Z]] | ||
| − | [[ | + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:TEL.pdf | Théorème des extrema liés]] |
| − | [[Média: | + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Bell.pdf | Nombres de Bell]] |
| − | [[ | + | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:ConvOn.pdf | Points extrémaux de la boule unité de L(E) ]] |
| − | [[ | + | * Théorème de d'Alembert-Gauss ([[Fichier:Tex.png|alt=Tex|link={{filepath:DAlembert-Gauss.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath: DAlembert-Gauss.pdf}} |24px]]) |
| − | + | == Développements d'informatique == | |
| − | [[ | + | * Langage de pile d'un automate à pile ([[Fichier:Tex.png|alt=Tex|link={{filepath:Dvt_langage_de_pile.tex}} |24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath:Dvt_langage_de_pile.pdf}} |24px]]) |
| + | * Arithmétique de Presburger ([[Fichier:Tex.png|alt=Tex|link={{filepath:Presburger.tex}}|24px]] ; [[Fichier:Pdf.png|alt=Tex|link={{filepath:Presburger.pdf}} |24px]]) | ||
| + | * [[Universalité d'un langage rationnel]] | ||
| + | * [[2SAT est décidable en temps linéaire]] | ||
| + | * [[Plus longue sous-séquence commune]] | ||
| + | * [[Automate des occurrences]] | ||
| + | * [[Hachage parfait]] | ||
| + | * [[Arbres binaires de recherche optimaux]] | ||
| + | * [[Problème de séparation par automates]] | ||
| + | * [[Théorème de Rice]] | ||
| + | * [[Fonction d'Ackermann]] | ||
| + | * [[Théorème de Higman]] | ||
Version actuelle en date du 27 janvier 2015 à 19:51
Certains d'entre nous tapent leurs développements. Vous pouvez, en plus des liens mis dans les pages leçons, les rassembler ici.
Pensez à ajouter les sources de vos développements : bien utile parfois !
Sommaire
Développements d'algèbre
Développements d'analyse
![]() Bernoulli et développement dyadique
Bernoulli et développement dyadique
![]() Le théorème de Weierstrass (via les polynômes de Bernstein)
Le théorème de Weierstrass (via les polynômes de Bernstein)
-> Le même résultat en passant par les probabilités : (![]() ,
, ![]() )
)
Théorème de Brouwer en dimension 2 (![]() ,
, ![]() )
)
![]() Un exemple de calcul d'intégrale
Un exemple de calcul d'intégrale
![]() Théorème de Cauchy-Arzela-Peano
Théorème de Cauchy-Arzela-Peano
Autour des variables aléatoires gaussiennes (![]() ,
, ![]() )
)
Projection dans un espace de Hilbert (![]() ,
, ![]() )
)
![]() Dérivée des fonctions lipschitziennes
Dérivée des fonctions lipschitziennes
![]() Méthode de Gauss d'approximation d'intégrale
Méthode de Gauss d'approximation d'intégrale
![]() Théorèmes d'Abel angulaire et taubérien faible
Théorèmes d'Abel angulaire et taubérien faible
![]() Formule sommatoire d'Euler Maclaurin
Formule sommatoire d'Euler Maclaurin
![]() Formule d'inversion de Fourier
Formule d'inversion de Fourier
Développements mixtes
![]() Surjectivité de l'exponentielle
Surjectivité de l'exponentielle
![]() Théorème de Cartan Von Neumann
Théorème de Cartan Von Neumann
![]() Convergence de la méthode de gradient à pas optimal (+Kantorovitch)
Convergence de la méthode de gradient à pas optimal (+Kantorovitch)
![]() Points extrémaux de la boule unité de L(E)
Points extrémaux de la boule unité de L(E)
Développements d'informatique
- Langage de pile d'un automate à pile (
 ;
;  )
) - Arithmétique de Presburger (
 ;
;  )
) - Universalité d'un langage rationnel
- 2SAT est décidable en temps linéaire
- Plus longue sous-séquence commune
- Automate des occurrences
- Hachage parfait
- Arbres binaires de recherche optimaux
- Problème de séparation par automates
- Théorème de Rice
- Fonction d'Ackermann
- Théorème de Higman
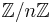 (
(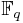 (
(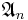 (
(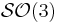 (
(