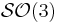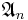Développements

Certains d'entre nous tapent leurs développements. Vous pouvez, en plus des liens mis dans les pages leçons, les rassembler ici.

Pensez à ajouter les sources de vos développements : bien utile parfois !

Développements d'algèbre

Sous groupes finis de ${\mathcal {SO}}(3)$

Groupe circulaire

Ellipse de Steiner

Commutant d'un endomorphisme. (Gwen : J'ai remplacé l'ancienne version par une moins succincte)

Groupes d'ordre 12

Simplicité de ${\mathfrak {A}}_{n}$

Caratheodory (and co)

Sylow

Automorphismes de ${\mathbb {Z}}/n{\mathbb {Z}}$

Polynômes irréductibles sur ${\mathbb {F}}_{q}$

Décomposition de Dunford et application à 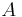$A$ diagonalisable 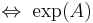$\Leftrightarrow \;\exp(A)$ diagonalisable

Théorème de l'élément primitif

Théorème de Hahn-Banach en dimension finie

Une version faible du théorème de Dirichlet

Réduction des matrices normales

Développements d'analyse

Méthode de Laplace

Prolongement de la fonction $\Gamma$

Bernoulli et développement dyadique

Ruine du joueur

Ellipsoïde de John-Loewner

Le théorème de Weierstrass (via les polynômes de Bernstein)

-> Le même résultat en passant par les probabilités : ( .tex, .pdf)

Le théorème de Glaeser

Lemme de Morse

Théorème de Brouwer en dimension 2

Lemme de Borel

Théorème d'Abel angulaire

Un exemple de calcul d'intégrale

Théorème de Cauchy-Arzela-Peano

Critère de Weyl

Dérivée des fonctions lipschitziennes

Formule des compléments

Théorème de stabilité de Lyapounov

Méthode de Gauss d'approximation d'intégrale

Développements mixtes

Lie-Kolchin

Surjectivité de l'exponentielle

Simplicité de SO(3)

[[Sous-groupes compacts de 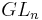$GL_{n}$]]

Théorème de Cartan Von Neumann

Convergence de la méthode de gradient à pas optimal (+Kantorovitch)

Théorème de Müntz